An Introduction to Graph Data Models
Publish Date: 2022-09-12
If we have to think about our world, society, IT, business, and social communication between peoples, use of machines and interactions with outside world. it is clear that we are in a connected world, and the internet makes all resources tie together.
Our world is full of relationships, and as a result of a search, we need models that can effectively model not just players, actors, or entities in a domain but also the relationship between them, as it turns out that exactly what graph databases are all about.
Graphs can be used to model many types of relations and processes in physical, biological, social and information systems.
in our article today, we will learn the basics concepts and terms of how data are modeled in graphs.
Graph as data theory
the concept of a graph is based on an already established subject in mathematics called
graph theory 1736-1936 .


This subject has algorithms for solving different types of real-world problems, and they are generally called graph algorithms.
What are Graphs
a graph is a mathematical data structure used to model the relationship between objects. The objects are called vertices or nodes, while the interconnection between is called an edge or a relationship (It could be an action that describes what nodes do or adjectives that qualifies the nodes or a grouping for that node )
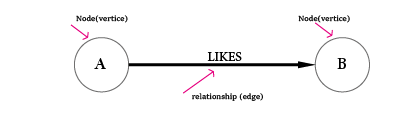
A graph it is not a chart, which is a visual representation of data.
Graph Model Terminology
the context of the relationship with nodes, determines how graph data are modeled. so, lets dive in more specific on how data can be represented as graph using vertices and edges.
Directed and Undirected graph
a directed graph is a graph where a relationship has a direction notation that qualifies this relation. For example the first graph: A Likes B, there is a direction :

but in this second graph, A and B are friends, there is no direction of relationship:

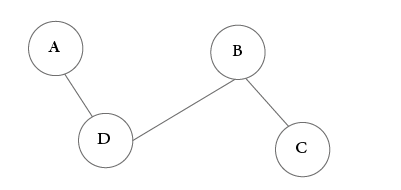
Connected and Disconnected graph
if we have a node that is connected to every node in the graph, and we can reach other nodes from that node, then we can say it is a connected graph.
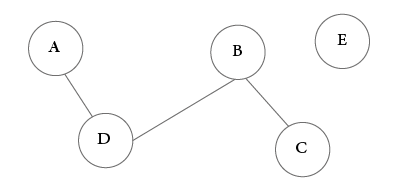
if there is an unreachable node (isolated from other nodes), then this is a disconnected graph:
Cyclic and Acyclic graph
Cyclic graph is a graph that contains at least one node has a path back to itself, so this graph is directed, and we call them Directed Cyclic Graphs (DCG) :
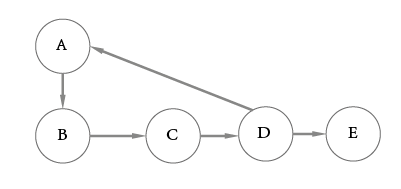
however an Acyclic does not have any node that has a path back to itself, we call them a Directed Acyclic Graph (DAG) :

Weighted and Unweighted graph
let us assume we have a graph of 2 nodes, if the edge (relationship) between them has an index or indication related to them, we call it a weighted graph.
for example, when you use any maps application on your mobile phone, there are some indications for roads that have traffic more than usual, this traffic is a weight:

but if this relationship can’t be differentiated from other edges or relationships, then we can say it is an unweighted graph.
for example, if you like a post of someone on social media, there is no concept of better like or double like, and it is the same for all edges in an unweighted graph.
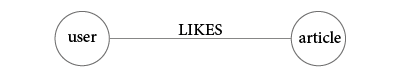
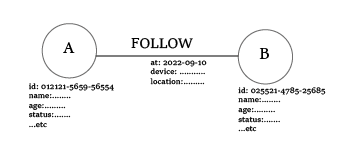
property graph
A graph within its nodes or relationships can have properties associated with them, and these properties are entirely schema-less, which means they can be present in some nodes and not in others, and the same for relationships.
Labeled Graph
graphs have labels to classify them. In graph nodes, all the nodes are modeled and created equally. so the node is a node, there is no concept of semi-node, full-node, or incomplete node.
But how to differentiate a user node from a post node? A tweet from a retweet node? It is a Label.
The label on the node or relationship classifies that. Think of it like a user node has a Label User, and this user has a relationship between Labeled Follow and other Labeled Like to make difference between them:
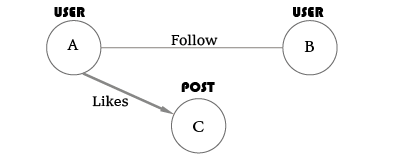
so Label means every node or relationship has a classification that helps us to identify what is going on in our graph database model.
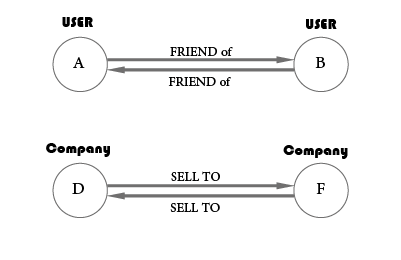
Parallel edges
if nodes in a graph have more than one relationship among them, we can say that our graph contains parallel edges. for example, people are friends of each other, or companies bought from each other products (double counting or spending):
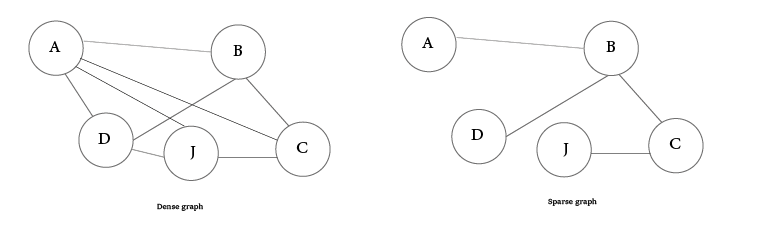
graph density
we can measure a graph density by looking at the number of vertices (nodes) relative to the number of edges (relationships).
So if a graph contains a small number of edges comparable to vertices then it is a sparse graph. otherwise, if vertices and edges are relatively close to each other or the edges are more (almost or fully connected), then it is a dense graph:
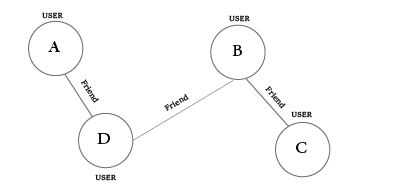
Mono Partite Graph
a graph is considered mono partite if we have only one type of label in our graph model. for example graph of friends like this picture shows:
Bi-Partite Graph
Bi means two, and if we have 2 labels in our graph, it should be no intra-relationship between them. which means no interconnection between vertices with same label can be found in a graph.
A typical example is a graph of ingredients and menus or recipes. So we will have nodes labeled ingredients, and other nodes labeled recipes. A recipe can be composed of many ingredients, and an ingredient can also be used in many recipes. however, we still don’t have relationships between ingredients among each other, or between recipes on another side. this picture show how that is possible in bi-partite graph:

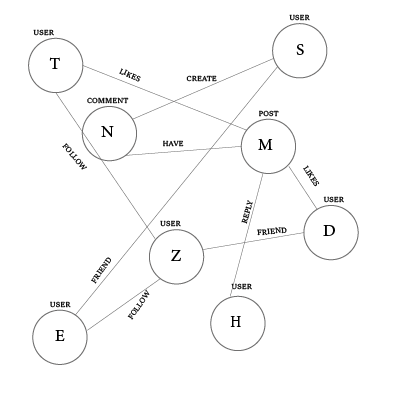
N-Parite Graph
is a graph that has 3 or more labels, for example, a graph containing: users, tweets, comments, posts...etc. the next figure shows an example of n partite graph
Multigraph
A multigraph is a graph that allows or contains self-loops (acoonection to a node itself), parallel edges, cyclic and acyclic, directed or undirected, connected as well as unconnected graphs. Also we can have a sub-graph, which is a graph within a graph.
the next figure all the types of graphs we discussed above , plus self loops which is
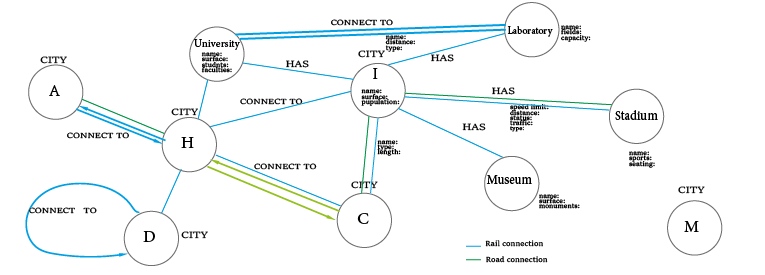
a multigraph graph is the real-world graphs available out there that we deal with on daily basis.
Conclusion
By the of this article I hope you are now familiar with graph data models and concepts.