Implement Selection Sort Algorithm
Publish Date: 2022-09-25

suppose you have a list of countries with their surface areas, and you want to sort them based on surface area, in descending order from the largest to smallest:
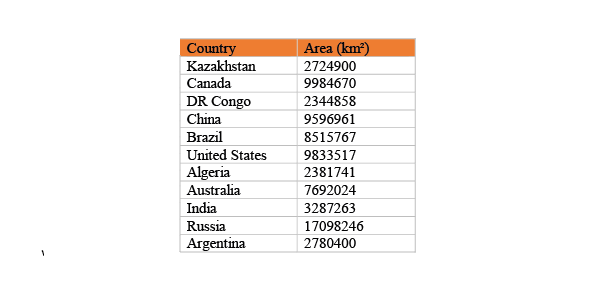
you want to sort this list from largess area to the smallest, how can you do that ?
One way is to go through the list and find the largest area, and add this country to the top of a new list:

Do the step again and find the largest area in the remaining items, and place it second after our new list:

Keep search and add items to the list, until you get all the countries sorted by area.
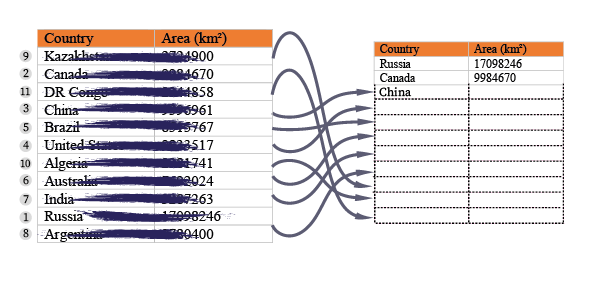
And this is how selection sort algorithm works in short.
Runtime
every time you are looking for the largest area in the list, you are searching the entire list, so a running time for the search is O(n). once you find the largest area, items will be (n-1) , and you keep repeating this step until you left only with one element which is the smallest. So, You check n elements, then n – 1, n - 2 … 2, 1. On average, you check a list that has 1 / 2 × n elements. Therefore, the runtime is: O(n × 1 / 2 × n) = O(n × n) = O(n²) . (constants like 1/2 are ignored in Big O notation) .Algorithm Implementation
there is multiples ways to implement selection sort algorithm between recursive and iterative paradigm. but for our case and to make things simple, we will implement the same way in example above. thus, We outline the selection sort algorithm first in 2 steps.
Python Implementation
1 - findLargest Function
we write a function findLargest that takes an array as input and find the largest element in it:
def findLargest(arr):
largest = arr[0]
largest_index = 0
for i in range(1, len(arr)):
if arr[i] > largest:
largest = arr[i]
largest_index = i
return largest_index
the principle on how this function works is quite simple: it chose and set an initial value at index 0:
largest = arr[0]
largest_index = 0
and compare it with each value in the array:
for i in range(1, len(arr)):
if arr[i] > largest:
and if the value in the array is larger than the first or previous one, update the index and the largest value as well:
largest = arr[i]
largest_index = i
and finally return the largest index to the next function:
return largest_index
2 - selectionSort Function
now in the selection sort method, we find the largest element in the array using the previous function:
for i in range(len(arr)):
largest = findLargest(arr)
we create an empty list:
newArr = []
and when we found the largest element, we remove it from the original array and append it to our new list in one step:
newArr.append(arr.pop(largest))
and finally, we return our new list sorted in descending order from largest to smallest:
return newArr
def selectionSort(arr):
newArr = []
for i in range(len(arr)):
largest = findLargest(arr)
newArr.append(arr.pop(largest))
return newArr
here is the full code in python:
def findLargest(arr):
largest = arr[0]
largest_index = 0
for i in range(1, len(arr)):
if arr[i] > largest:
largest = arr[i]
largest_index = i
return largest_index
def selectionSort(arr):
newArr = []
for i in range(len(arr)):
largest = findLargest(arr)
newArr.append(arr.pop(largest))
return newArr
to test out our code, let’s test it on IPython session using a small list:
def findLargest(arr):
...: largest = arr[0]
...: largest_index = 0
...: for i in range(1, len(arr)):
...: if arr[i] > largest:
...: largest = arr[i]
...: largest_index = i
...: return largest_index
...:
def selectionSort(arr):
...: newArr = []
...: for i in range(len(arr)):
...: largest = findLargest(arr)
...: newArr.append(arr.pop(largest))
...: return newArr
...:
list1 = [100, 2, 58, 10, 70, 5, 150]
print(selectionSort(list1))
[150, 100, 70, 58, 10, 5, 2]
to test it in our 'countries' area list:
areas = [2724900, 9984670, 2344858, 9596961, 8515767, 9833517, 2381741, 7692024, 3287263, 17098246, 2780400]
print(selectionSort(areas))
[17098246, 9984670, 9833517, 9596961, 8515767, 7692024, 3287263, 2780400, 2724900, 2381741, 2344858]
Scala Implementation
because Scala is considered as a strong functional programming language, it uses immutable objects by default, but in our case we have to use mutable collections to make our solution consistent.
The next steps is implemented in scala repl.
So we will use array buffers and list buffers instead of arrays and list to support our implementation:
import scala.collection.mutable.{ArrayBuffer, ListBuffer}
import scala.collection.mutable.{ArrayBuffer, ListBuffer}
here is the findLargest method:
def findLargest(array: ArrayBuffer[Int]): Int = {
| var largest: Int = array(0)
| var largest_index: Int = 0
| for (i <- 1 to array.length - 1) {
| if (array(i) > largest) {
| largest = array(i)
| largest_index = i
| }
| }
| largest_index
| }
findLargest: (array: scala.collection.mutable.ArrayBuffer[Int])Int
and for the function selectionSort:
def selectionSort(array: ArrayBuffer[Int]) = {
| var newArr = ListBuffer[Int]()
| for (i <- array) {
| val largest_index = findLargest(array)
| newArr += array.remove(largest_index)
| }
| newArr
| }
selectionSort: (array: scala.collection.mutable.ArrayBuffer[Int])scala.collection.mutable.ListBuffer[Int]
now if we test our algorithm on a simple array:
val list1:ArrayBuffer[Int] = ArrayBuffer(100, 2, 58, 120,10, 70, 5, 150,16)
list1: scala.collection.mutable.ArrayBuffer[Int] = ArrayBuffer(100, 2, 58, 120, 10, 70, 5, 150, 16)
println(selectionSort(list1))
ListBuffer(150, 120, 100, 70, 58, 16, 10, 5, 2)
if we execute the code on our area list, it would give results s expected:
val areas:ArrayBuffer[Int] = ArrayBuffer(2724900, 9984670, 2344858, 9596961, 8515767, 9833517, 2381741, 7692024, 3287263, 17098246, 2780400)
areas: scala.collection.mutable.ArrayBuffer[Int] = ArrayBuffer(2724900, 9984670, 2344858, 9596961, 8515767, 9833517, 2381741, 7692024, 3287263, 17098246, 2780400)
println(selectionSort(areas))
ListBuffer(17098246, 9984670, 9833517, 9596961, 8515767, 7692024, 3287263, 2780400, 2724900, 2381741, 2344858)
if you prefer working with editor, here is the full code:
import scala.collection.mutable.{ArrayBuffer, ListBuffer}
object SelectionSort {
def findLargest(array: ArrayBuffer[Int]): Int = {
var largest: Int = array(0)
var largest_index: Int = 0
for (i <- 1 to array.length - 1) {
if (array(i) > largest) {
largest = array(i)
largest_index = i
}
}
largest_index
}
def selectionSort(array: ArrayBuffer[Int]) = {
var newArr = ListBuffer[Int]()
for (i <- array) {
val largest_index = findLargest(array)
newArr += array.remove(largest_index)
}
newArr
}
def main(args: Array[String]): Unit = {
val list1:ArrayBuffer[Int] = ArrayBuffer(100, 2, 58, 120,10, 70, 5, 150,16)
println(selectionSort(list1))
val areas:ArrayBuffer[Int] = ArrayBuffer(2724900, 9984670, 2344858, 9596961, 8515767, 9833517, 2381741, 7692024, 3287263, 17098246, 2780400)
println(selectionSort(areas))
}
}
ListBuffer(150, 120, 100, 70, 58, 16, 10, 5, 2)
ListBuffer(17098246, 9984670, 9833517, 9596961, 8515767, 7692024, 3287263, 2780400, 2724900, 2381741, 2344858)
Process finished with exit code 0
Java Implementation
java implementation is quite similar to scala, we use mutable collections. in that case we use ArrayList for data retrieval and manipulations, and LinkedList to append new values.
here is the findLargest method in java:
however, we cannot remove element from arrays while we iterate through it. so we need to use iterator instead.
the code of selectionSort would be like that:
Conclusion
Now after executing the above Java program you would have understood how Selection Sort works & how to implement it in Java, Scala, as well as Python. I hope this article is informative and added value to you. Thus we have come to an end of this article on ‘Selection Sort Algorithm’.