The principles of Heuristic Function and GPS coordinates

Publish Date: 2022-10-20

---

In sphere we have no strait lines, so the distance between 2 points on the surface of sphere measured by geodesics which is circles whose centers coincide with the center of the sphere, and they are called great circles.

Between antipodal points (directly opposite each other ), there are infinitely many great circles, and all great circle arcs between antipodal points have a length of half the circumference ( the perimeter of a circle) of the circle, or pr , where r is the radius of the sphere.

Before moving further let’s define the symbols we will use in our demo:

• r: is the sphere's radius; any line from the center to a point on the sphere is also called a radius.
• σ : represent the summation
• θ : theta is Commonly used as a variable to indicate an angle.
• λ: Lambda is used as abbreviation for the longitude
• φ: phi is used as abbreviation for the "latitude"
• ∆ : delta Represents a small change

Great Distance

let’s say we have 2 points P, Q that we want to calculate a distance between those two points using their geographical latitude φ and longitude λ .

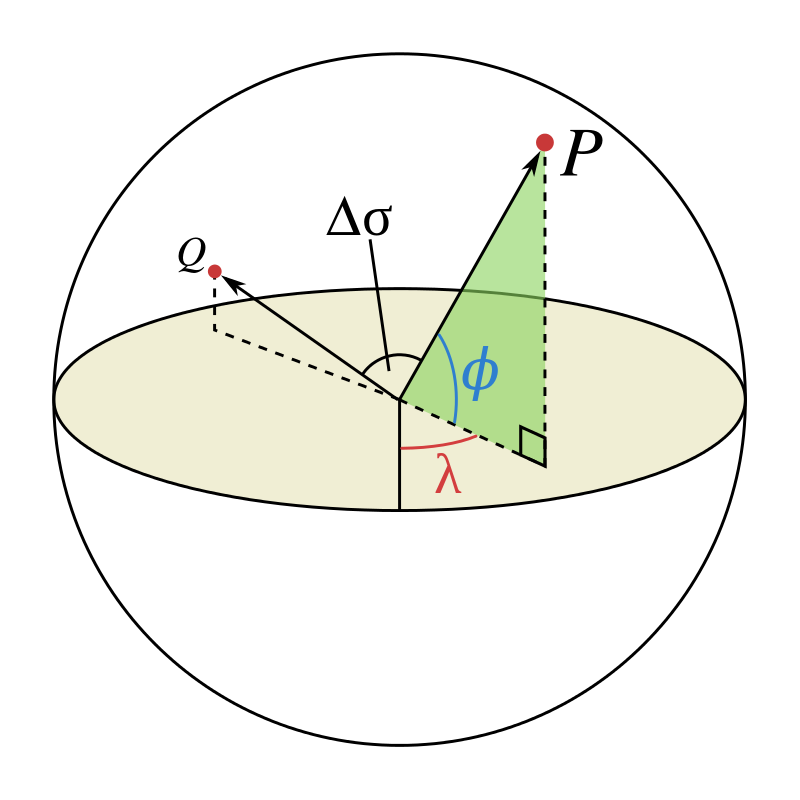
we have the coordinate of P(φ₁,λ₁) and Q(φ₂,λ₂). ∆φ,∆λ their absolute differences. then the central angle between them ∆σ , is given by the spherical law of cosines:

given the angle in radians , the distance d between two points P and Q along a section of curve (arc length) on sphere of radius is:

if the two points are too small at the surface of the Earth, the cosine of the central angle is near 0.99999999, which can cause rounding error. (https://en.wikipedia.org/wiki/Great-circle_distance#cite_note-3 (

The haversine formula is numerically better-conditioned for small distances .

The Haversine Formula

The haversine formula determines the great-circle distance between two points on a sphere given their longitudes and latitudes. Important in navigation, it is a special case of a more general formula in spherical trigonometry, the law of haversines, that relates the sides and angles of spherical triangles.

for two points on a sphere, the central angle θ can be calculated using the radius and the distance :

The versine of an angle is 1 minus its cosine. so we can get haversine/versine of θ ( hav(θ) ) using latitude φ and longitude λ of two points P(φ₁,λ₁) and Q(φ₂,λ₂) :

Note: the "Ha" in "Haversine" stands for "half versed sine" where haversin(θ) = versin(θ)/2.

if we apply that function to both the central angle θ and the differences in latitude and longitude, the haversine function hav(θ) would be:

as the haversine function computes half a versine of angle θ and in order to find the distance d, we need to apply the arcsine to our haversine function:

to simplify a formula, let's set the insider subset formula to a:

then our formula would be like that:

and since our angles need to be in radians(not in degrees) and we have to use atan (arctan) function which two points as difference , so our final formula would be:

this formula is only an approximation when applied to the Earth, which is not a perfect sphere. the "Earth radius" R varies from 6356.752 km at the poles to 6378.137 km at the equator. More importantly, the radius of curvature of a north-south line on the earth's surface is 1% greater at the poles (≈6399.594 km) than at the equator (≈6335.439 km)—so the haversine formula cannot be guaranteed correct to better than 0.5%.

Example

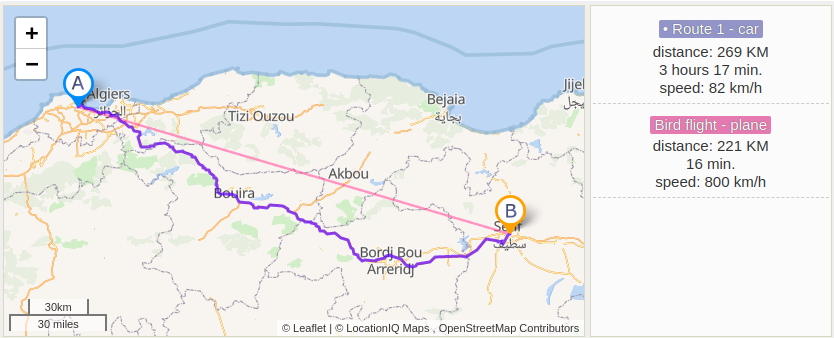
let's say we want to calculate the distance between Setif and Algiers cities. we have these coordinate points:

• Algiers(36.7530171, 3.04185570)
• Setif(36.18898, 5.414416)

note: don't forget to convert into radians where 1° × π/180 = 0,01745rad .

if we apply the above final formula using those coordinates. and given r is the earth at equator line at average has a value equal = 6371 km and for A(φ1=36.7530171, λ1=3.04185570) and S(φ2=36.18898,λ2=5.414416), we will end up at d(A,S) = 271.1 km in distance.

you can calculate yourself to verify or use the python implementation, to make it easy for you.

>

here is the implementation of haversine formula as a python function to calculate the distance, you only need to input the longitude and latitude and the function will find the distance for you in meters and kilometers:

# the haversine formula
def haversine(coord1: object, coord2: object):
    import math
    # Coordinates in decimal degrees (e.g. 2.89078, 12.79797)
    lon1, lat1 = coord1
    lon2, lat2 = coord2
    r = 6371  # radius of Earth in kilometers

    # convert values to radians
    phi_1 = math.radians(lat1)
    phi_2 = math.radians(lat2)
    delta_phi = math.radians(lat2 - lat1)
    delta_lambda = math.radians(lon2 - lon1)

    a = math.sin(delta_phi / 2.0) ** 2 + math.cos(phi_1) * math.cos(phi_2) * math.sin(delta_lambda / 2.0) ** 2
    d = r * 2 * math.atan2(math.sqrt(a), math.sqrt(1 - a))

    distance_km = d  # output distance in meters
    distance_meters = distance_km * 1000.0  # output distance in kilometers

    distance_km = round(distance_km, 3)
    distance_meters = round(distance_meters, 3)

    print(f"Distance: {distance_km} km")
    print(f"Distance: {distance_meters} m")


# Algiers(φ1=36.7530171, λ1=3.04185570)
# Setif(φ2=36.18898,λ2=5.414416)
haversine([36.7530171, 3.04185570], [36.18898, 5.414416])

and here is the output:

Distance: 271128.8249293379 m
Distance: 271.129 km

Process finished with exit code 0

and here is the map calculation, which is very close to our program output :

Longitude and latitude

so far, we have been talking about finding distance between two point in sphere using their longitude and latitude , but we did not see how to find those measurements for a given point and what does it mean really.

The latitude

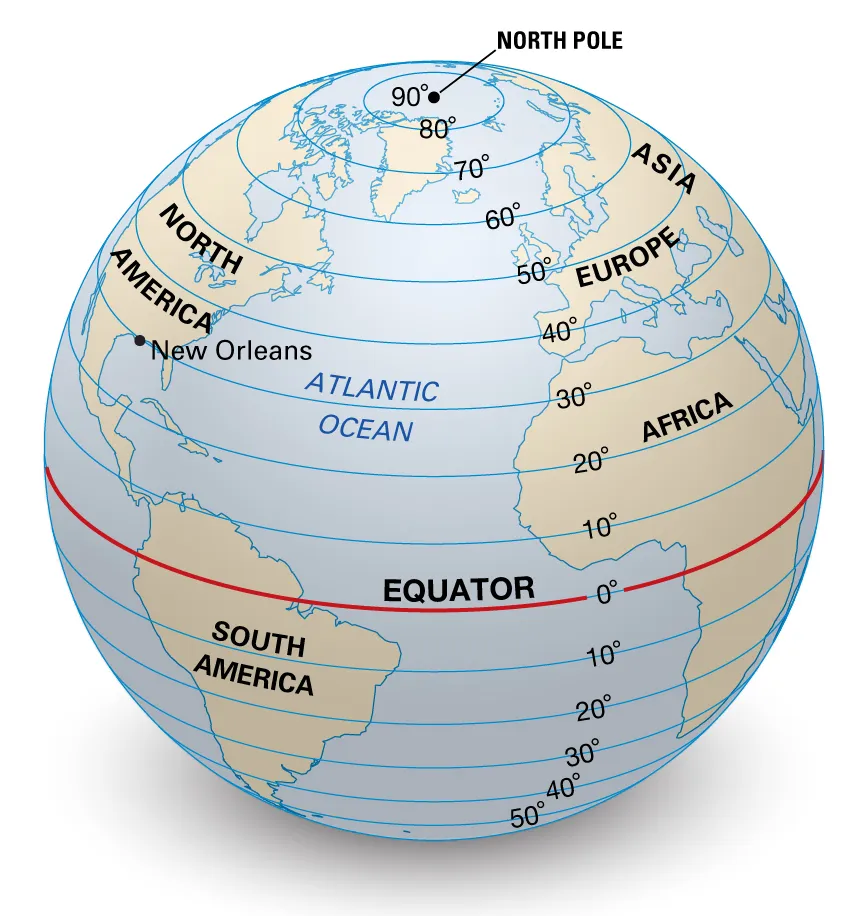
the latitude is a measurement that specify the position of a point on Earth’s surface and how far that point from north or south off the equator . The Equator has a latitude of 0°, the North Pole has a latitude of 90° North (written 90° N or +90°), and the South Pole has a latitude of 90° South (written 90° S or −90°). The Equator divides the globe into Northern and Southern Hemispheres.

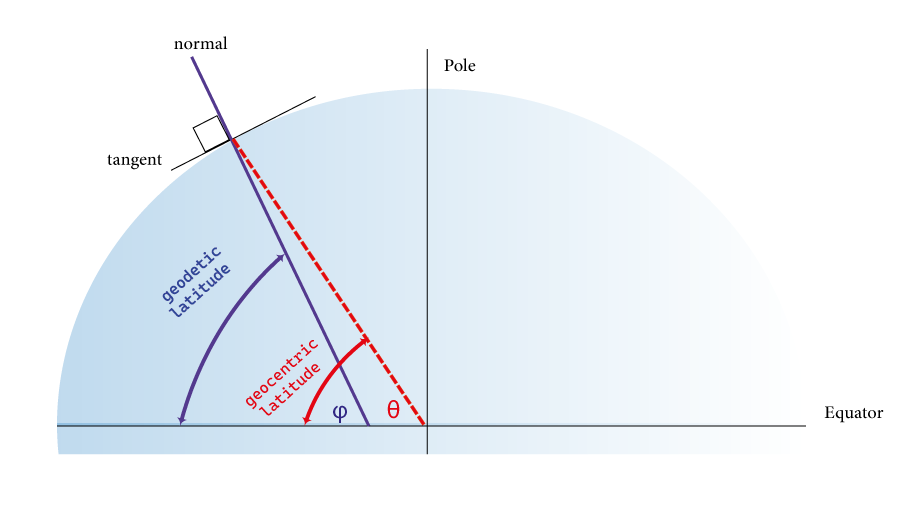
there is different kinds' latitude (geocentric, astronomical, and geographic( i.e: geodetic)). The geocentric latitude is the angle between the equatorial plane and the radius from the center (of Earth) to a point of interest. Whereas Geodetic latitude is defined as the angle between the equatorial plane and the normal to the surface at that point. When used without qualification, the term latitude refers to geodetic latitude.

As we know, the earth radius ranges from a maximum of nearly 6,378 km (3,963 mi) (equatorial radius) to a minimum of nearly 6,357 km (3,950 mi) (polar radius). So, The length of a degree of arc of latitude is approximately 111 km (69 miles), varying, because of the non uniformity of Earth’s curvature, from 110.567 km (68.706 miles) at the Equator to 111.699 km (69.41 miles) at the poles.

For example Algiers city have latitude of 36.7530171, which means it is approximately 4079.58 km far from the equator.

The Longitude

Longitude is a measurement of location or point, to east or west of the prime meridian at Greenwich, (London, England), the specially designated imaginary north-south line that passes through both geographic poles and Greenwich.

Longitude is measured 180° both east and west of the prime meridian. Which means all the location points at the Prime Meridian has a Longitude of 0°, and the locations from Prime Meridian to the east have the longitude between 0° and 180° East (written 180° E or +180°), and the locations west to Prime meridian has a longitude between 0° and 180° West (written 180° W or −180°).

This is not to be conflated with the International Date Line (IDL) , which diverges from it in several places for political and convenience reasons, including between far eastern Russia and the far western Aleutian Islands.

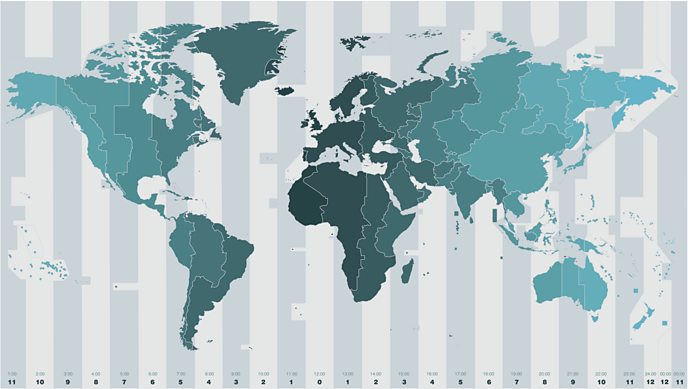
The map above shows the 24 time zones across the world.

The distance per degree of longitude at the Equator is about 111.32 km (69.18 miles) and at the poles is, 0. For example Algiers city have longitude of 3.04185570°, which means approximately it is 338.619 km far from the Prime Meridian to the east.

Earth's graticule for latitude and longitude

The combination of both longitude and latitude specifies the position of any location on the surface of Earth, without consideration of altitude or depth. The visual grid on a map formed by lines of latitude and longitude is known as a graticule. The origin/zero point of this system (where Prime Meridian and the Equator meet) is located in the Gulf of Guinea about 625 km (390 mi) south of Tema, Ghana, a location often facetiously called Null Island.

Lines of latitude and longitude form a grid pattern on a globe. The lines mark the unique location of every place on Earth:

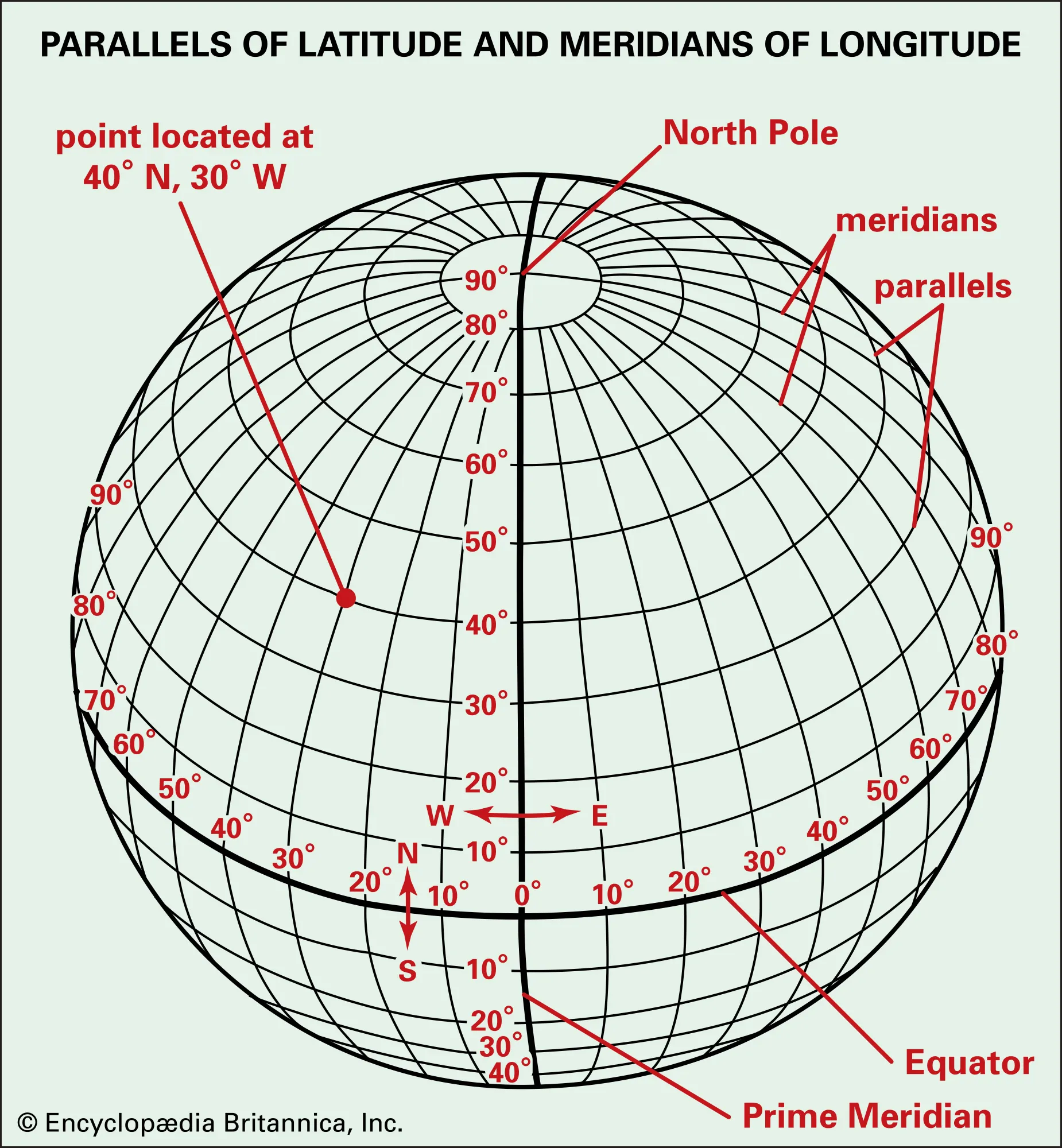
The vertical lines from pole to pole are lines of constant longitude, or meridians. The circles parallel to the equator are lines of constant latitude, or parallels. The graticule shows the latitude and longitude of points on the surface. In this example meridians are spaced at 6° intervals and parallels at 4° intervals :

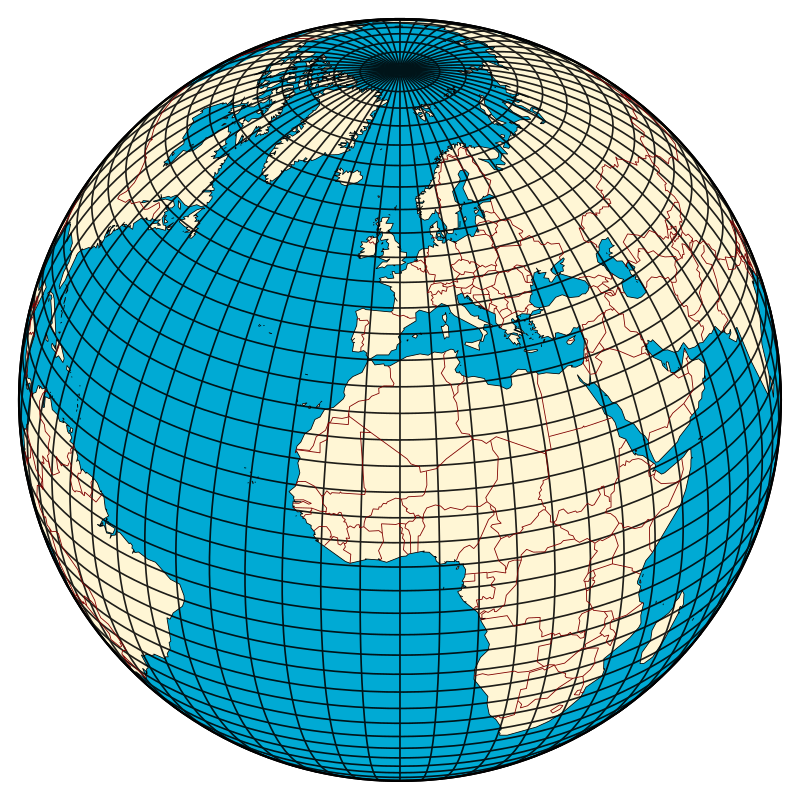
For example if we want to define the Algiers city from our Earth graticule, we move first from the equator until the exact position of Algiers, that is it 9 great circles plus a small step which result in approximately 36° and almost 3/4 degree , that equal to 36.75°.

Then we calculate the distance from the prime meridian , which is about half distance before the next first meridian line , that is 6/3 which result in 3° degrees as shown in the next figure:

the modern systems give an exact location into meter perimeters, and for algiers city it has the GPS coordinates GPS (Latitude/ Longitude): Algiers (36.7530171, 3.04185570).

and you can find other cities coordinates using the same concept.

Final Thoughts

The system of latitude and longitude, also called parallels and meridians, is based on 360 degrees.

The Earth is nearly spherical, so great-circle distance formulas give the distance between points on the surface of the Earth correct to within about 0.5%.

Resources

• hawaii.edu
• glsed.co.uk
• bbc.co.uk
• geogarage.com
• distances-routieres
• esri.com
• britannica.com
• Admiralty Manual of Navigation, Volume 1, The Stationery Office, 1987, p. 10, ISBN 9780117728806, .

---